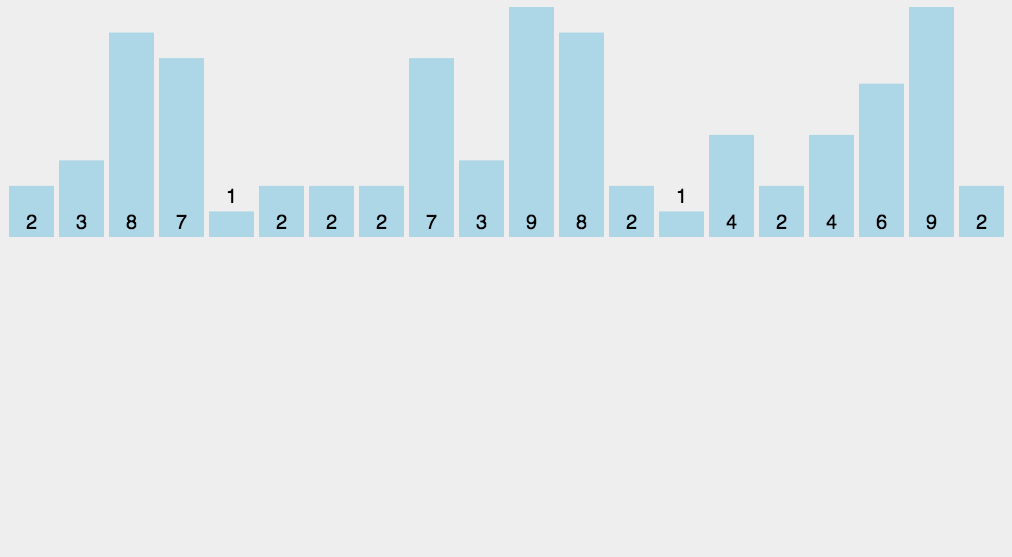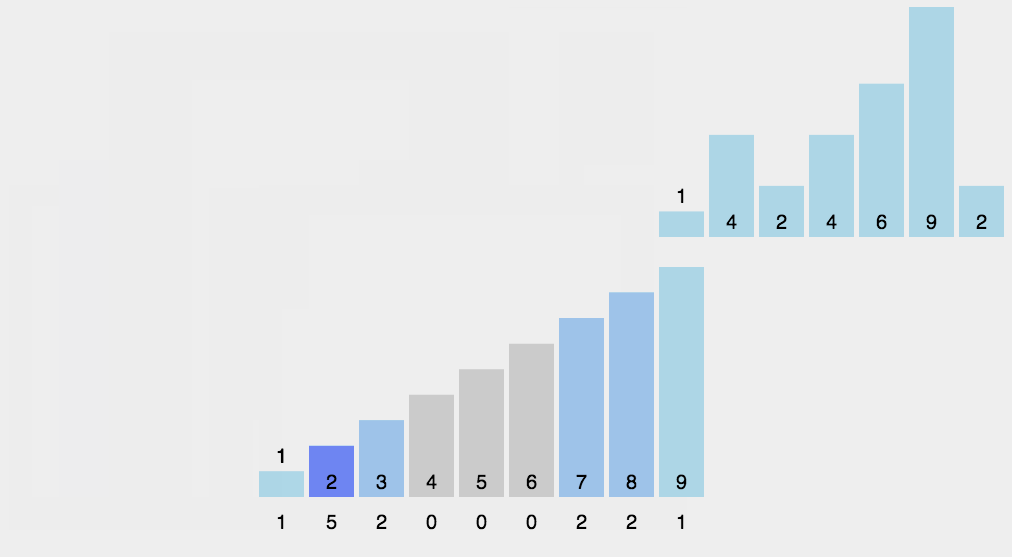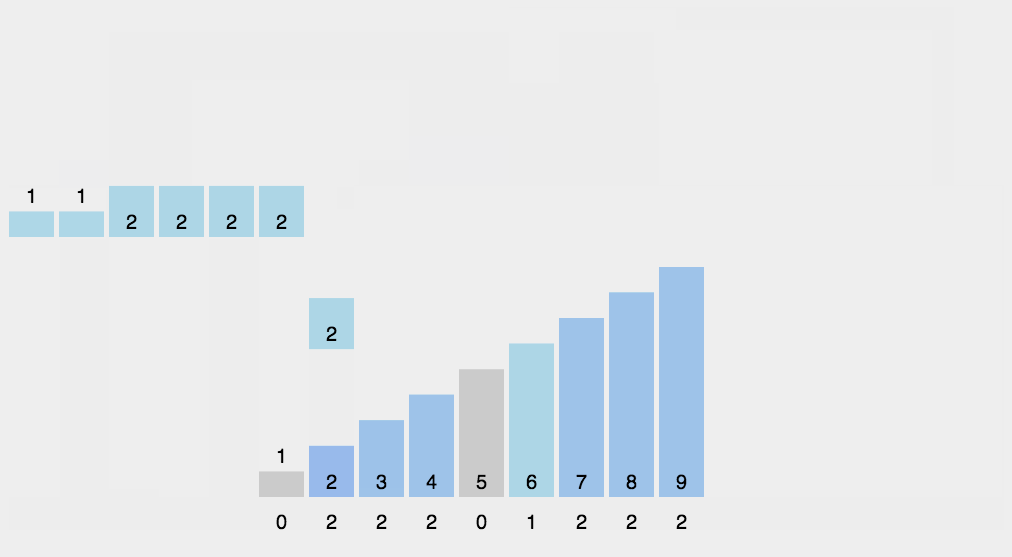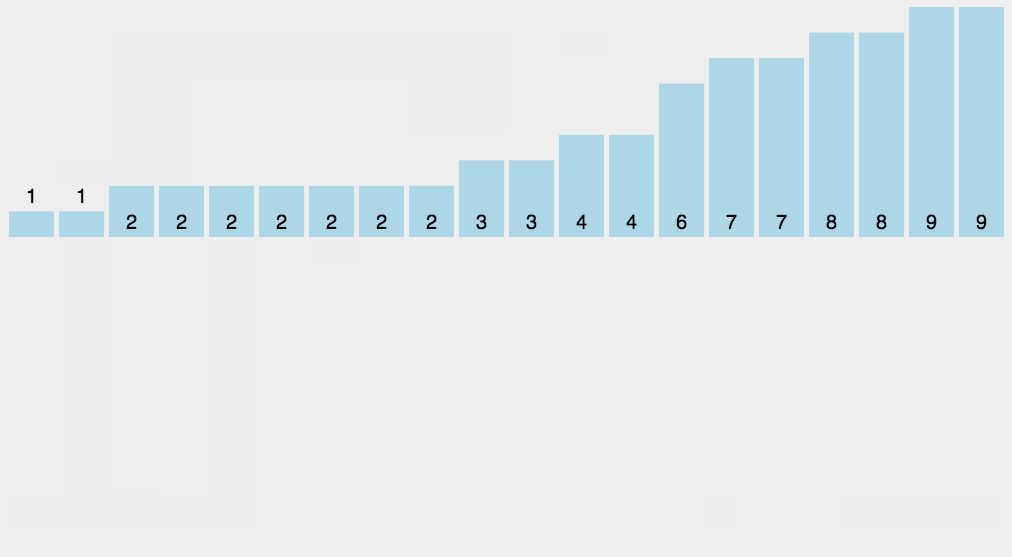概述
计数排序不是基于比较的排序算法,其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数
算法描述
- 找出待排序的数组中最大和最小的元素
- 统计数组中每个值为i的元素出现的次数,存入数组C的第i项
- 对所有的计数累加(从C中的第一个元素开始,每一项和前一项相加)
- 反向填充目标数组:将每个元素i放在新数组的第C(i)项,每放一个元素就将C(i)减去1
动图演示
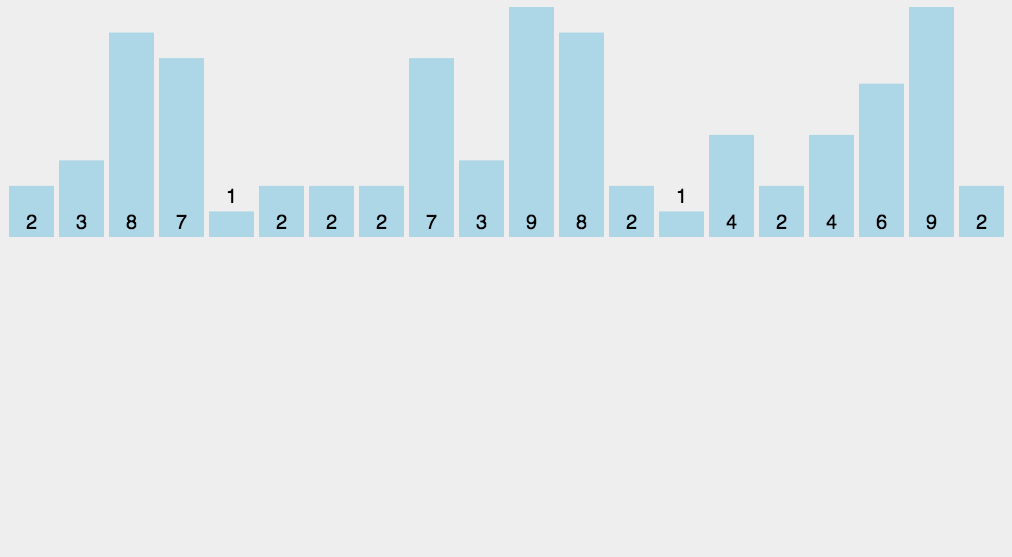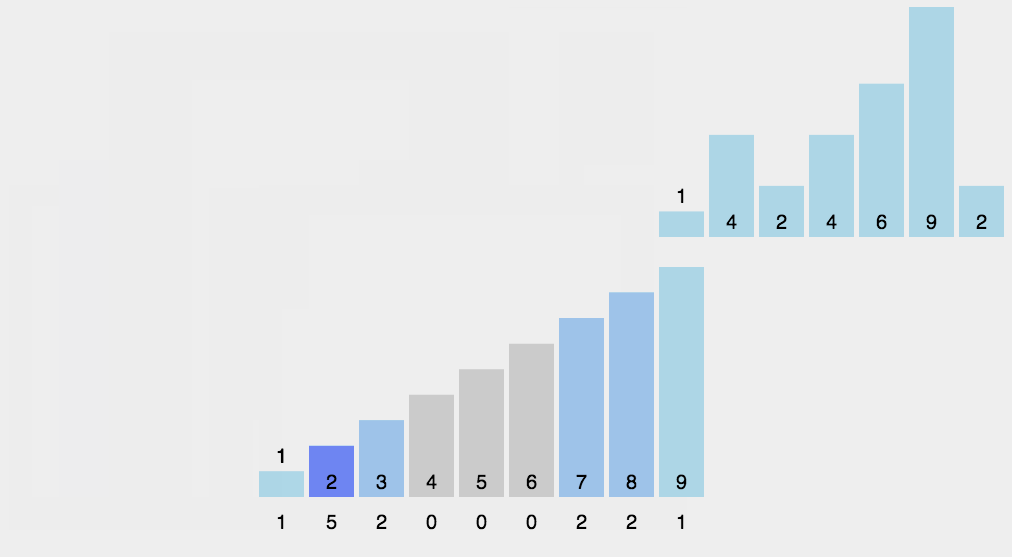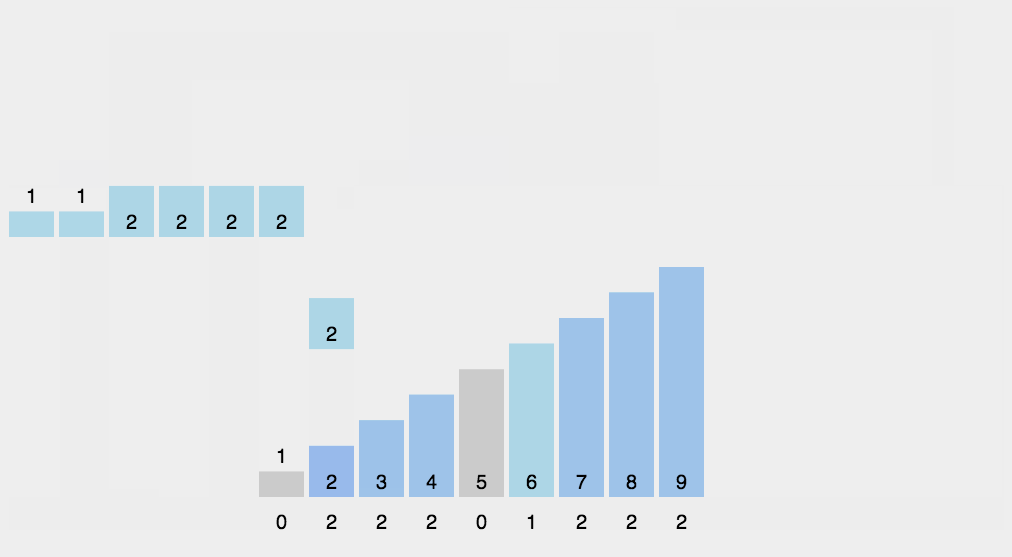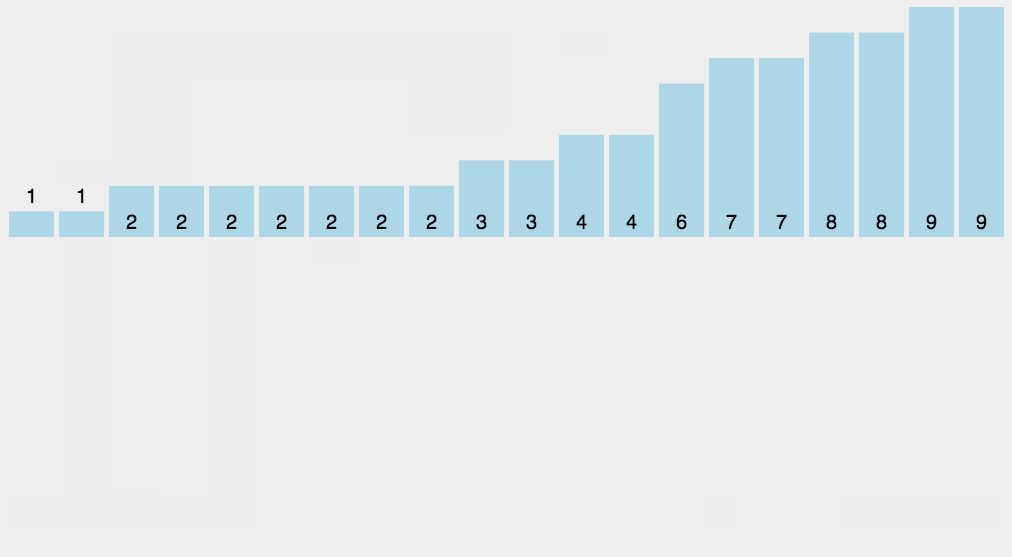
算法实现
Java代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
public class Test {
public static void main(String[] args)
{
int[] A=new int[]{2,5,3,0,2,3,0,3};
int[] B=countSort(A, 5);
System.out.println("排序前:");
for (int i : A) {
System.out.print(i+" ");
}
System.out.println();
System.out.println("排序后:");
for (int i : B) {
System.out.print(i+" ");
}
}
private static int[] countSort(int[] array,int k)
{
int[] C=new int[k+1];
int length=array.length,sum=0;
int[] B=new int[length];
for(int i=0;i=0;i--)
{
B[C[array[i]]-1]=array[i];
C[array[i]]--;
}
return B;
}
}
|
运行结果
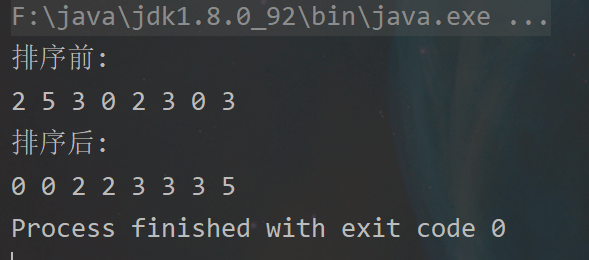
算法分析
计数排序是一个稳定的排序算法。当输入的元素是 n 个 0到 k 之间的整数时,时间复杂度是O(n+k),空间复杂度也是O(n+k),其排序速度快于任何比较排序算法。当k不是很大并且序列比较集中时,计数排序是一个很有效的排序算法
PS.
搬运地址: 十大经典排序算法(动图演示) - 一像素 - 博客园 (cnblogs.com)